베르누이 방정식은 관속을 흐르는 유체의 압력과 속도, 수두를 구할 때 이용합니다.

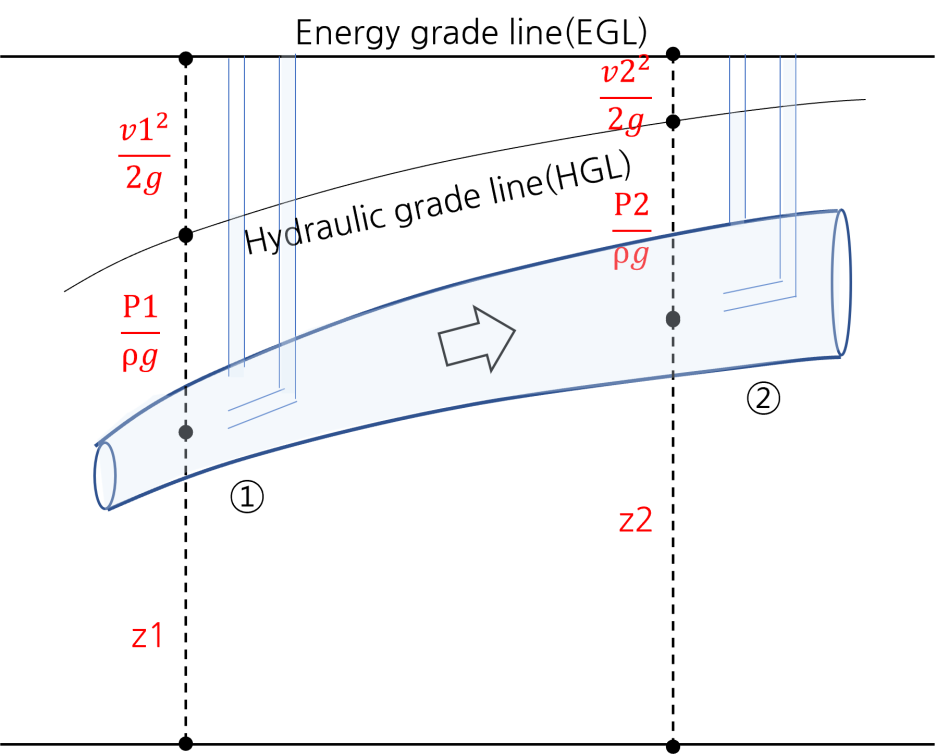
베르누이 방정식

베르누이 방정식은 유체의 흐름이 정상상태(steady flow)로써 유체의 속도가 시간에 따라 변하지 않고 일정한 흐름이며, 마찰손실이 없는 상태에서의 유체 흐름에 대한 방정식입니다.

베르누이 방정식은 관속을 흐르는 유체의 각 지점의 에너지 총합이 같다는 것으로써 에너지 보존 법칙에 대한 것입니다. 관속을 흐르는 유체의 에너지는 중력에 의한 위치에너지, 유체가 배관에 작용하는 압력에너지, 유체가 이동하는 과정에서 생기는 운동에너지의 합으로 설명됩니다.

유체가 배관에 작용하는 압력을 정압이라고 하고 유체가 이동할 때 이동방향으로 작용하는 압력을 동압이라고 합니다.

1지점에서의 유체 에너지 총량 = 2지점에서의 유체 에너지 총량

위치에너지 1+ 압력에너지 1 + 운동에너지 1 = 위치에너지 2 + 압력에너지 2 + 운동에너지 2

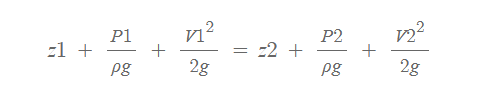
위의 식은 수두(m) 단위로 표현된 베르누이 방정식입니다. 수두는 물기둥 높이를 m로 나타낸 것으로 압력을 다른 형태로 표현한 것입니다. 펌프의 양정을 구할 때 수두 단위로 계산을 합니다.

유체의 압력을 구하는 공식은 위와 같은데 높이 h 는 베르누이 방정식에서 z와 같습니다. 그래서 수두 h (z)는

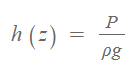
로 표현됩니다. 유체가 수직으로 작용하는 압력은 유체의 양과는 상관 없이 유체 높이 (수두)에 대한 함수 입니다. 예를 들어, 대기압은 1atm = 1bar = 10mAq 로 물기둥 10m 높이의 압력과 같습니다.

배관을 흐르는 유체의 속도가 바뀌면 압력도 바뀌며 두 지점의 수두의 합이 같기 때문에 어떤 지점의 속도와 압력을 알면 다른 지점의 유체속도를 구할 수 있습니다.

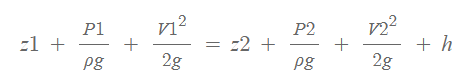
베르누이 방정식은 마찰손실이 없다고 가정했습니다. 하지만 실제로는 마찰손실이 존재하고 마찰손실에 의한 수두는 위 식의 h 값과 같이 표현됩니다.

베르누이 방정식의 가정

1) 1차원 정상유동이다.

2) 유선의 방향으로 흐른다.

3) 외력은 중력과 압력만이 작용한다.

4) 비점성, 비압축성 유동이다.

5) 마찰력에 의한 손실은 무시한다.

배관이나 덕트를 설계할 때 마찰압력손실이 일정하도록 하고 길이를 산출한 후 마찰손실을 곱해서 정압손실(pressure drop) 값을 구합니다. 이렇게 구한 정압손실의 총합과 유량을 가지고 송풍기 또는 펌프 모델을 선정합니다. 만일, 송풍기나 펌프가 잘못 선정되어 실제 현장에서 운전했을 때 측정된 정압손실이 설계 정압손실 보다 큰 경우에는 원하는 유량이 공급되지 않게 되고 결국 원하는 만큼의 열교환을 못하는 문제가 발생합니다.

여기까지 베르누이 방정식에 대해서 알아보았습니다.